De hecho r² es igual a +1 siempre que la
línea de regresión sea un estimador
perfecto.
Una segunda forma extrema en la que las
variables X y
Y pueden relacionarse es aquella en que los puntos podrían
caer a distancias iguales en ambos lados de una línea de
regresión horizontal. A continuación mostramos la
gráfica:
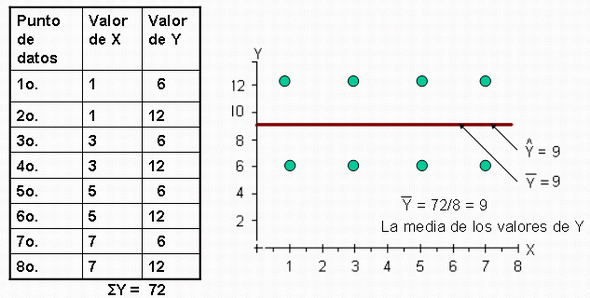


Sustituimos los valores en
la fórmula encontramos que el coeficiente de
determinación de muestra es igual
a 0

Por lo tanto el valor de
r² es cero cuando no hay correlación.
Un r² cercano a 1 indica una fuerte
correlación entre X y Y.
Un r² cercano a 0 indica que existe poca
correlación entre X y Y.
Se debe subrayar fuertemente que r² mide solo la
fuerza de una
relación lineal entre 2 variables. Por ejemplo, si
tuviéramos muchos puntos X y Y y todos cayeran en la
circunferencia de un círculo, aunque dispersos
aleatoriamente, claramente habría una relación
entre estos puntos. (todos caen en el mismo
círculo),
Pero si calculamos r² resultaría estar cerca
de 0, porque los puntos no tienen una relación lineal
entre sí.
Para evitar estos cálculos, los
estadísticos han desarrollado una versión de
atajo, usando los valores que
habríamos determinado de antemano en el análisis de regresión.
La fórmula es:

Para ver que esta fórmula es un atajo, la
aplicaremos a nuestra anterior regresión que relaciona los
gastos de
inversión y desarrollo con
las ganancias. Recuerde que cuando encontramos los valores para a
y b la línea de regresión para este problema
es:
![]()



3,600 + 2,000 – 5,400
= ——————————-
5,642 – 5,400
200
= —— = 0.826 Coeficiente de determinación
de muestra
242
Por tanto, podemos concluir que la variación
en los gastos de investigación y desarrollo (la variable
independiente X) explica 82.6 % de la variación en las
ganancias anuales (la variable dependiente Y)
Coeficiente
de correlación.
Es la segunda medida que podemos usar para describir que
tan bien una variable es explicada por otra.
Cuando tratamos con muestras el coeficiente de
correlación de muestra se denota como r y es la
raíz cuadrada del coeficiente de determinación de
muestra: r = √r²
Cuando la pendiente de la ecuación de
estimación es positiva, r es la raíz cuadrada
positiva, pero si b es negativa, r es la √
negativa.
El signo de r indica la dirección de la relación entre las
dos variables X y Y.
Diversas características de r, el coeficiente
de correlación de muestra

En el problema anterior encontramos que el
Coeficiente de determinación de muestra es r² =
0.826, para encontrar r sustituimos este valor en la
ecuación:
r = √r²
= √0.826
= 0.909 Coeficiente de correlación de
muestra
La relación entre las dos variables es directa
y la pendiente es positiva, por tanto el signo de r es
positivo.
Supongamos que la cantidad gastada en boletos de
cine
correlaciona 0.6 con el ingreso familiar. A primera vista, 0.6
parece ser una correlación bastante fuerte ya que esta
más cerca de 1 que de 0. Pero esto explica sólo el
36% (0.6 x 0.6 = 0.36) de la variación en la cantidad de
dinero que las
familias gastan en películas. Esto sugiere que una
estrategia de
comercialización diseñada para
atraer familias con altos ingresos
pasaría por alto una gran cantidad de clientes
potenciales.
Desarrollo en
Minitab.
CORRELACION
1.- Abrir el Minitab.
2.- Introducir los datos en la hoja
de trabajo

3.- Colocarse en el siguiente Menú y
opción:
Stat Basic Statistics
Correlation

4.- Seleccionar las variables a
correlacionar:
Gastos y Ganancias dando clic en cada una hasta que
aparezcan en el recuadro de variables, posteriormente dar clic
en el botón OK.


5.- Minitab calcula el resultado utilizando la
Correlación de Pearson.
Donde en este caso tenemos una correlación de
.909 que como se explicó anteriormente nos indica que los
Gastos de Investigación y las ganancias están
correlacionados.
El p-value (valor de probabilidad) nos
indica la siguiente hipótesis:
Ho: cuando p-value > 0.05
H1: cuando p-value < 0.05

DIAGRAMA DE
DISPERSIÓN.
- Para generar el diagrama de
dispersión:
Colocarse en el siguiente Menú y
opción:
Graph Scatterplot

2.- Seleccione la opción Con Regresión.
(With Regression) y dar clic en OK

3. Seleccionar las variables de Gastos y Ganancias con
un clic.


y posteriormente clic en OK para obtener la siguiente
gráfica de dispersión:

LÍNEA DE
REGRESIÓN Y ECUACIÓN DE
REGRESIÓN.
1.- Para generar el diagrama de dispersión con
la línea de regresión y la ecuación de
regresión: Colocarse en el siguiente Menú y
opción:
Stat Regression Fitted Line
Plot…

2.- Seleccionar las variables Y y X y clic
OK.

Se desplegará la siguiente gráfica que
representa la función Y
= 20 + 2X

Desarrollo de
un Caso.
Una agencia de Viajes desea
saber la relación que hay entre las ventas, el
presupuesto
destinado a publicidad, y las
comisiones de los vendedores para esto presenta los siguientes
datos. Realice los análisis respectivos.

ANÁLISIS DE DATOS:
Se van a utilizar las siguientes
variables:
Variables
Independientes:
1.- Gastos de Publicidad
2.- Comisión de vendedores
Variable dependiente:
– Ventas

De acuerdo a los cuadros podemos
decir:
– La variable que más relación tiene con la
Variable Dependiente es decir las ventas es la variable Gastos
de Publicidad
– En cuanto a la variable Comisiones
de vendedores podemos decir que no tiene
relación relevante con las
Ventas.
La variable que más relación tiene con las
ventas es la variable Gastos de Publicidad.

– En cuanto a la variable Comisiones de vendedores
podemos decir que no tiene relación relevante con las
Ventas:

Bibliografía:
Estadística para Administradores,
Richard I. Levin y David S. Rubin.
Editorial Prentice Hall
Equipo integrado por:
Ing. Gerardo Valdes Fuentes
gerardo.valdes.fuentes[arroba]gmail.com
Ing. Rosa Isela Meléndez
López
Lic. José Luis Chávez
Dávila
Ing. Renato Elmer Vázquez
García
Maestría en Administración y Liderazgo.
Universidad Autónoma del Noreste.
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |